- Estimating Avogadro's Number Lab Answers
- Determining Avogadro's Number Lab Report
- Calculating Avogadro's Number
- Estimating Avogadro's Number Lab
- Calculating Avogadro's Number Calculator
Start by calculating the volume of one mole of solid Al =(26.98 g/mol)/(2.70 g/mL)= 9.99 mL/mol. According to the packing density, only 0.74 og this is atoms (the rest is empty space), so the volume of the atoms alone is (9.99 mL/mol)x0.74 = 7.39.


- Key Points The mole allows scientists to calculate the number of elementary entities (usually atoms or molecules) in a certain mass of a given substance. Avogadro’s number is an absolute number: there are 6.022×10 23 elementary entities in 1 mole. This can also be written as 6.022×10 23 mol -1.
- Calculating Avogadro’s number Number of stearic acid molecules / Moles of stearic acid A number = N molecules / M A number = (1.76 x 10 16 molecules) / (.000000320 moles) A number = 5.50 x 10 22 molecules Trial 2 calculations Calculating length of thread used C = (l Circle) x 2 So, C = (11.2 cm) x 2 C = 22.4 cm Calculating radius.
- However, in its 26th Conference, the BIPM adopted a different approach: effective 20 May 2019, it defined the Avogadro number as the exact value N = 6.022 140 76 × 1023, and redefined the mole as the amount of a substance under consideration that contains N constituent particles of the substance.
- The number of units in one mole of any substance is called Avogadro’s number or Avogadro’s constant. It is equal to 6.022140857×10 23. The units may be electrons, ions, atoms, or molecules, depending on the character of the reaction and the nature of the substance.
2 H+(aq) + 2 electrons -> H2(g)
This experiment is based on the mass loss of the copper anode, but it is also possible to collect the hydrogen gas that is evolved and use it to calculate Avogadro's number.
- Direct current source (battery or power supply)
- Insulated wires and possibly alligator clips to connect the cells
- 2 Electrodes (e.g., strips of copper, nickel, zinc, or iron)
- 250-ml beaker of 0.5 M H2SO4 (sulfuric acid)
- Water
- Alcohol (e.g., methanol or isopropyl alcohol)
- Small beaker of 6 M HNO3 (nitric acid)
- Ammeter or multimeter
- Stopwatch
- Analytical balance capable of measuring to nearest 0.0001 gram
Current(average): 0.601 amperes (amp)
Time of electrolysis: 1802 seconds (s)
one ampere = 1 coulomb/second or one amp.s = 1 coul
charge of one electron is 1.602 x 10-19 coulomb
- Find the total charge passed through the circuit.
(0.601 amp)(1 coul/1amp-s)(1802 s) = 1083 coul - Calculate the number of electrons in the electrolysis.
(1083 coul)(1 electron/1.6022 x 1019coul) = 6.759 x 1021 electrons - Determine the number of copper atoms lost from the anode.
The electrolysis process consumes two electrons per copper ion formed. Thus, the number of copper (II) ions formed is half the number of electrons.
Number of Cu2+ ions = ½ number of electrons measured
Number of Cu2+ ions = (6.752 x 1021 electrons)(1 Cu2+ / 2 electrons)
Number of Cu2+ ions = 3.380 x 1021 Cu2+ ions - Calculate the number of copper ions per gram of copper from the number of copper ions above and the mass of copper ions produced.
The mass of the copper ions produced is equal to the mass loss of the anode. (The mass of the electrons is so small as to be negligible, so the mass of the copper (II) ions is the same as the mass of copper atoms.)
mass loss of electrode = mass of Cu2+ ions = 0.3554 g
3.380 x 1021 Cu2+ ions / 0.3544g = 9.510 x 1021 Cu2+ ions/g = 9.510 x 1021 Cu atoms/g - Calculate the number of copper atoms in a mole of copper, 63.546 grams.
Cu atoms/mole of Cu = (9.510 x 1021 copper atoms/g copper)(63.546 g/mole copper)
Cu atoms/mole of Cu = 6.040 x 1023 copper atoms/mole of copper
This is the student's measured value of Avogaro's number! - Calculate percent error.
Absolute error: |6.02 x 1023 - 6.04 x 1023 | = 2 x 1021
Percent error: (2 x 10 21 / 6.02 x 10 23)(100) = 0.3 %
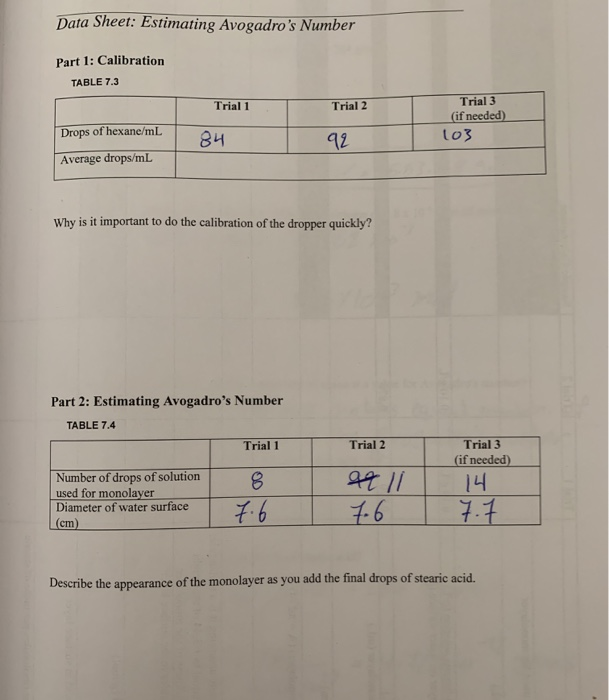
Estimating Avogadro's Number Lab Answers
Contrary to the beliefs of generations of chemistry students, Avogadro’s number—the number of particles in a unit known as a mole—was not discovered by Amadeo Avogadro (1776-1856). Avogadro was a lawyer who became interested in mathematics and physics, and in 1820 he became the first professor of physics in Italy. Avogadro is most famous for his hypothesis that equal volumes of different gases at the same temperature and pressure contain the same number of particles.
Determining Avogadro's Number Lab Report
The first person to estimate the actual number of particles in a given amount of a substance was Josef Loschmidt, an Austrian high school teacher who later became a professor at the University of Vienna. In 1865 Loschmidt used kinetic molecular theory to estimate the number of particles in one cubic centimeter of gas at standard conditions. This quantity is now known as the Loschmidt constant, and the accepted value of this constant is 2.6867773 x 1025 m-3.
Calculating Avogadro's Number
The term “Avogadro’s number” was first used by French physicist Jean Baptiste Perrin. In 1909 Perrin reported an estimate of Avogadro’s number based on his work on Brownian motion—the random movement of microscopic particles suspended in a liquid or gas. In the years since then, a variety of techniques have been used to estimate the magnitude of this fundamental constant.
Estimating Avogadro's Number Lab
Accurate determinations of Avogadro’s number require the measurement of a single quantity on both the atomic and macroscopic scales using the same unit of measurement. This became possible for the first time when American physicist Robert Millikan measured the charge on an electron. The charge on a mole of electrons had been known for some time and is the constant called the Faraday. The best estimate of the value of a Faraday, according to the National Institute of Standards and Technology (NIST), is 96,485.3383 coulombs per mole of electrons. The best estimate of the charge on an electron based on modern experiments is 1.60217653 x 10-19 coulombs per electron. If you divide the charge on a mole of electrons by the charge on a single electron you obtain a value of Avogadro’s number of 6.02214154 x 1023 particles per mole.
Calculating Avogadro's Number Calculator
Another approach to determining Avogadro’s number starts with careful measurements of the density of an ultrapure sample of a material on the macroscopic scale. The density of this material on the atomic scale is then measured by using x-ray diffraction techniques to determine the number of atoms per unit cell in the crystal and the distance between the equivalent points that define the unit cell (see Physical Review Letters, 1974, 33, 464).
